嫌いな教科＆好きな教科1位の「算数・数学」を好きになる方法

とはどんなものでしょう？

本書は、「パート1・嘆き」と「パート2・喜び」の2部構成。「パート1」で、現在の算数・数学教育がいかにつまらないかを語り尽くし、「パート2」ではいよいよ「数学の魅力」が披露されます。

一例として、「奇数を足すと」の項を見てみましょう。

著者はまず、「奇数を小さいものから順番に足してみよう」と読者を誘います。

1+3＝4

1+3+5＝9

1+3+5+7＝16

1+3+5+7+9＝25

すると出てきた答えは4、9、16、25。これはそれぞれ2、3、4、5の平方数（2乗）です。つまり、1から順に奇数を足していくとその答えは「足した数字の個数の2乗」になるということに気づきます。

著者のいう「本当の数学」はここから。この法則がいつまでも続くのか、なぜ奇数を足すと「足した数字の個数の2乗」になるのかを証明することです。

そして試行錯誤の結果、著者は1枚のイラストでそれを証明することに成功します。



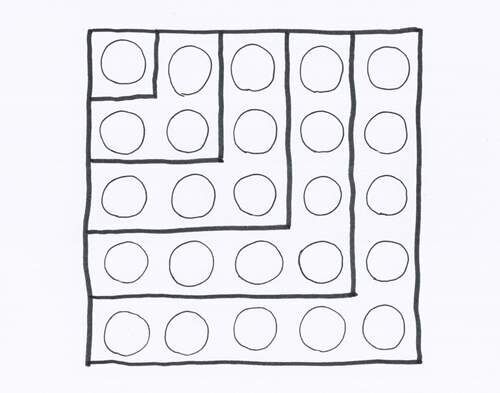
どうでしょう、5×5の正方形の中には、ちゃんと1、3、5、7、9が入っています。

この図は、奇数を足すと「足した数字の個数の2乗」になるという法則が“パターン”になっていて、いつまでも続くものであることを証明しています。